Máximos y mínimos

En algunas aplicaciones de la derivada es necesario determinar, cuando la función tiene un valor máximo o un valor mínimo. En lo siguiente, consideraremos que la función que se analiza es derivable al menos 2 veces.

Sea la función  y = 4x – x², la gráfica que se muestra en la figura. De la misma se deduce que el valor máximo de la curva está en x = 2, es decir, en el punto  y = 4 que es el valor máximo de la función.

Como el valor de la derivada en cualquier punto de una curva es igual a la pendiente de la recta tangente es ese punto; sin recurrir a la gráfica se puede hallar el valor de x mediante el siguiente procedimiento:

1. - Obtener el valor de la derivada de la función

2. - Igualar a cero la ecuación que resulta.

3. - Resolver la ecuación para hallar el valor crítico de x.

4. - Sustituir el valor crítico de x en la función dada y encontrar el valor de f(x).

5. - Tomar un valor ligeramente mayor y otro ligeramente menor que el valor crítico de x y sustituir en la derivada de la función.

6. - Si la pendiente resulta con un valor (+)  a (-) entonces, se trata de un máximo, y si cambia de (-) a (+) entonces es un mínimo.

Ejemplo: Encontrar el valor máximo o mínimo de la función  y = 4x – x²

Siguiendo los tres pasos anteriores, tenemos

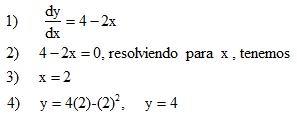
Tomar dos valores, uno ligeramente mayor y otro ligeramente menor que x = 2

Para x = 1.9   dy/dx = 4 – 2 (1.9) = 0.2    es positivo

Para x = 2.1    dy/dx  = 4 – 2 (2.1) = -0. 2  es negativo

Se observa que hay un cambio en la pendiente de la recta de (+) a (-) entonces la curva pasa de creciente a decreciente por lo que se deduce que la curva presenta un punto máximo.

Ejemplo:  Determinar si la gráfica de la función y = x² – 3x + 6 presenta un máximo o un mínimo, mediante el método de la derivada.

Siguiendo el procedimiento anterior

1)                   dy/dx = 2x – 3

2)                    2x – 3 = 0,  donde x = 3/2 = 1.5

3)                    Tomar dos valores cercanos a x = 3/2

Para x = 1    dy/dx = 2(1) – 3 = 3 – 2 = -1   es negativo

Para x = 2    dy/dx = 2(2) – 3 =  4 – 3 = 0   es positivo

La gráfica va de negativo a positivo, entonces la gráfica presenta un valor mínimo; va de decreciente a creciente.

Para conocer la coordenada en y del valor mínimo; sustituimos x  = 3/2 en la función:

y = (3/2)² – 3(3/2) + 6, de donde y = 15/4

Concavidad y puntos de inflexión

Analicemos la siguiente figura:

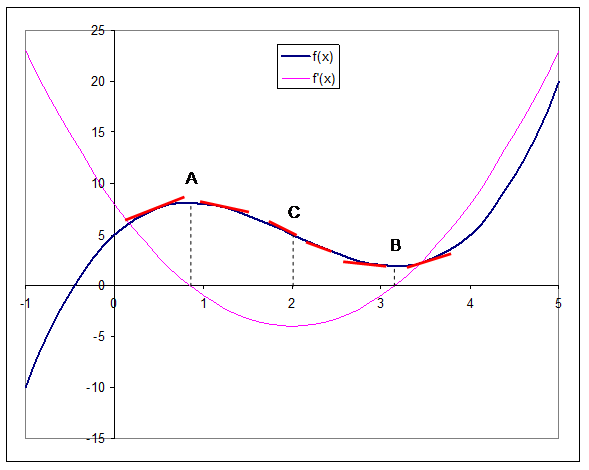
Dada una curva de ecuación y = f(x) con primera derivada igual a 0 en un punto A y en un punto B:

Si la pendiente de la derivada de f(x) es ( + )  a la izquierda y ( - ) a la derecha del punto A, entonces la curva tiene un valor máximo, se dice que la curva es cóncava hacia abajo.

Si la pendiente de una recta tangente a esa curva es (-) a la izquierda y (+) a la derecha del punto B, entonces la curva presenta un mínimo, la curva es cóncava hacia arriba.

Si la pendiente de una recta tangente a la curva tiene el mismo signo a ambos lados de un punto, como en C, pero cambia su sentido de crecimiento (pasa de crecer a decrecer o viceversa), entonces, la curva solo cambia el sentido de la concavidad y por tanto no presenta un máximo ni mínimo. Se trata de un punto de inflexión. En ese punto la función que representa la primera derivada, como se muestra en la figura, tiene un punto crítico. ¿Qué valor tendrá la segunda derivada? Evidentemente debe ser 0.

Es bueno aclarar que este hecho de que la segunda derivada sea 0, es condición necesaria pero no suficiente para que exista un punto de inflexión. Puede darse el caso de que la segunda derivada en un punto sea 0 y no haya punto de inflexión. Considere por ejemplo la función y = x²ⁿ, evaluada en x = 0.

Calculo de puntos críticos de una función utilizando la segunda derivada.

Indiscutiblemente este es el procedimiento a elegir normalmente. El método consiste en encontrar la primera y segunda derivada de la función, siguiendo los pasos que a continuación se enumeran:

I.-  Hallar la primera derivada de la función

II.-  Igualar a cero la primera derivada y resolver la ecuación para determinar los valores críticos.

III.-  Obtener la segunda derivada de la función.

IV.-  Sustituir en la segunda derivada cada uno de los valores críticos obtenidos. Si el resultado es negativo se tendrá un máximo y si es positivo se tendrá un mínimo.

Si la segunda derivada en un punto es 0 y la tercera derivada es desigual de 0, tendremos un punto de inflexión.

Ejemplos: Hallar los máximos y mínimos de cada función empleando el método de la segunda derivada.

a)     y = x⁴ + 32x

I.-   y’ = 4x³ + 32  ;

II.-  0 = 4x³ + 32  ;  x³ = 32/4;  x³ = 8;  x = 2 valor crítico:

III.- y’’ = 12x²; 

IV.- y’’ = 12 (2)²   y’’ = 48 éste valor es positivo, entonces, el valor es un mínimo.

b)   y = x³ – 2x² + x

I.- y’ = 3x² – 4x + 1: 

II.- 0 = 3x² – 4x + 1  factorizando (x – 1) (3x – 1) = 0  con dos puntos críticos: x₁ = 1 y  x₂ = 1/3

III.- y’’ = 6x – 4                               

IV.-

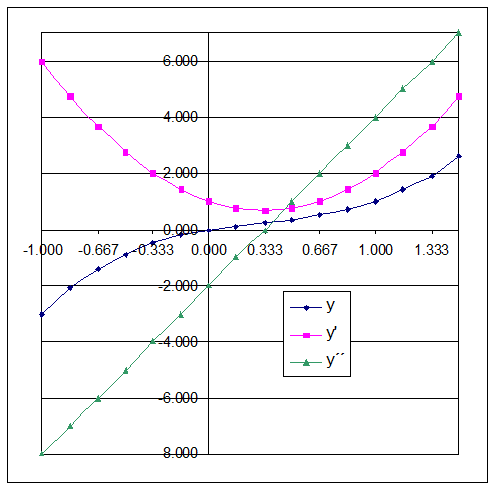
Ejemplo de un punto de inflexión: para la función y = x³-x²+x

Los ejercicios que se muestran a continuación serán discutidos en clase.

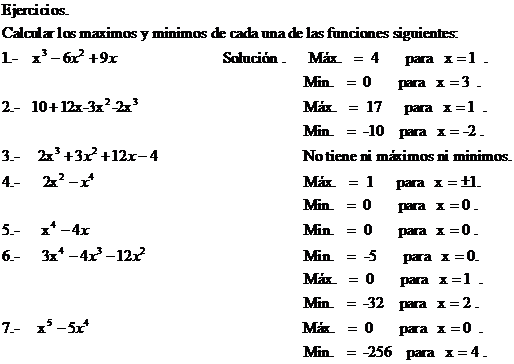
Enlace a material didáctico sobre máximos y mínimos (en inglés).

Enlace a página con ejercicios de máximos y mínimos (contiene anuncios).

REGRESAR