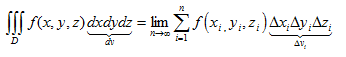
Para el cálculo de las integrales triples partiremos de la definición de integral triple que es similar a la de integral doble, solo que ahora consideraremos una tercera variable:
Si f(x,y,z) es continua en un recinto D del espacio R3, tal que D = {(x,y,z) Î R3 |a £ x £ b, c £ y £ d, e £ z £ f, entonces la integral triple de f sobre D, se define como:
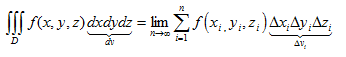
siempre que exista el límite. Nótese que el elemento de volumen es dV = dx dy dz.
Tomando en cuenta las consideraciones de continuidad para f(x,y,z) y las consecuencias posteriores de integrabilidad similares a las hechas para la integral doble, se tiene que la integral triple sobre el paralelepípedo D de la función f(x,y,z) se puede expresar como:
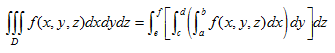
Como se puede observar se utilizan integrales iteradas. Para las mismas también se cumple el teorema de Fubini, o sea se puede cambiar el orden de integración obteniéndose el mismo resultado.
Ejemplo. Sea D = [0,1]×[0,2]×[0; 3] y f(x,y,z) = xyz. Entonces:
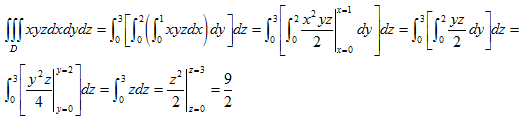
Ejercicio a entregar por escrito: cambiar el orden de integración y comprobar que se obtiene el mismo resultado.
Al igual que se hizo para las integrales dobles, se extienden estos conceptos a recintos más generales, acotados por funciones que se definen en función de las variables de la manera siguiente:
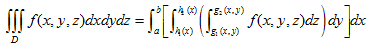
Nótese que integramos entre 2 funciones de x e y que acotan los valores de z, posteriormente entre dos funciones de x que acotan los valores de y y finalmente entre los valores de a y b que acotan a la variable x. Si consideramos otro orden de integración hay que hacer las correspondientes consideraciones sobre las funciones que acotan los valores de cada variable.
Ejemplo: Calcular la integral triple de f(x,y,z) = xy en la región definida por
D = {(x,y,z) Î R3 |x2+y2+z2 £ 1, x ³ 0, y ³ 0, z ³ 0.
R/ Nótese que la región de integración es la parte de la esfera de centro en el origen de coordenadas y radio 1 que está contenida en el primer octante, que se muestra en la siguiente figura:
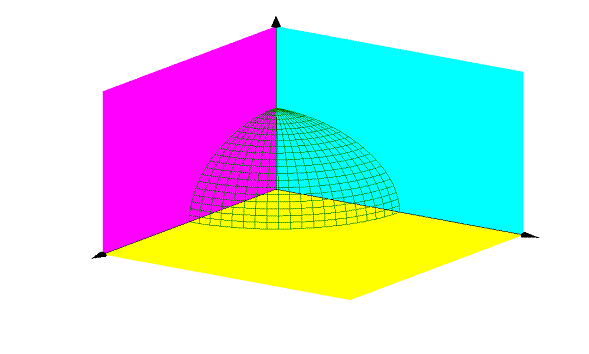
Entonces los límites de integración serán: z entre 0 y √1- x2 – y2 ; y entre 0 y 1 - x2 ; x entre 0 y 1. Entonces:
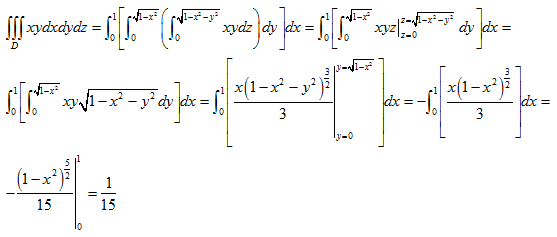
Aplicaciones de las integrales triples
La principal aplicación de las integrales triples es en la determinación de volúmenes. Correspondientemente, si se conoce la función de la densidad de un cuerpo en función de las coordenadas, es posible hallar la masa de una porción del cuerpo acotada por determinadas funciones. Esto permite a su vez el cálculo de momentos de inercia, etc. Pueden consultar un documento en PDF tomado de:
http://caminos.udc.es/info/asignaturas/obras_publicas/203/pdfs/aplics_int_triples.pdf
Ilustraremos la determinación de volúmenes utilizando las fórmulas para hallar integrales triples en coordenadas cilíndricas y esféricas.
Es importante recordar las fórmulas de transformación de coordenadas cilíndricas a coordenadas cartesians y las expresiones que ya se vieron de los elementos diferenciales de volumen: x = rcosq; y = r senq; z = z ; dV = rdrdqdz. La deducción del diferencial de volumen la pueden encontrar en una página de Khan Academy si solicitan la explicación. Entonces si f es una función continua en una región R del espacio, tenemos:
![]()
![]()
R/
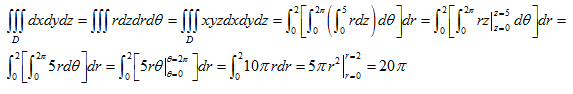
Nótese que el resultado es exactamente el que se esperaba, el volumen de un cilindro de radio 2 y altura 5.
Es importante recordar las fórmulas de transformación de coordenadas cartesianas a coordenadas esféricas y las expresiones que ya se vieron de los elementos diferenciales de volumen: x = rsenfcosq; y = rsenfsenq; z = rcosf; dV = r2senfdqdfdr. La deducción del elemento diferencial de volumen la pueden encontrar en una página de Khan Academy. Entonces si f es una función continua en una región R del espacio, tenemos:
![]()
![]()
R/
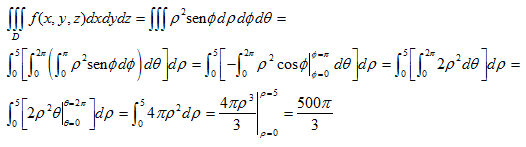
Y el resultado es el esperado, o sea el volumen de una esfera de radio 5.
Para alcanzar las habilidades en el cálculo de integrales triples, acceda a un grupo de ejercicios resueltos (en PDF), tomados de
http://www.ehu.es/~mtpalezp/libros/05_4.pdf
Finalmente, pueden consultar un resumen sintético (en pdf) de las integrales múltiples en una página de un profesor de la Universidad Autónoma de Madrid. También pueden ver el tema completo y ejemplos resueltos en una página de la Universidad Nacional de la Plata.