
Conceptos básicos
Recordemos algunas definiciones que fueron vistas en Matemáticas I:
Variable: Es un símbolo (x, y, z, m, n, o, etc.), que representa un elemento no específicado de un conjunto dado. Dicho conjunto es llamado universo de la variable y cada elemento del conjunto es una posible variable. Por ejemplo si x es una variable cuyo universo es el conjunto C = {1,2,3,4}, x puede tomar cualquiera de los valores de ese conjunto.
Constante: Es un símbolo que denomina al elemnto de un conjunto que tiene sólo un elemento, o sea tiene un valor fijo.
Parámetro: son constantes pero para una familia de ecuaciones (curvas), funcionan como variables. Por ejemplo en y = ax+b, a y b son parámetros de esa familia de rectas.
Par ordenado: Es un conjunto de dos elementos (x,y), donde x es la primera componente y y la segunda componente. Por ejemplo en (2,5), la primera componente es 2 y la segunda componente es 5. En nuestro curso, casi siempre lo asociaremos con las coordenadas de un punto en coordenadas cartesianas. El par ordenado (a,b) es desigual a (b,a). Esto se ve en el ejemplo gráfico de que (5,3) es desigual a (3,5):

Funciones
En las matemáticas superiores el concepto de función es esencial. En su desarrollo intervinieron destacados matemáticos como Descartes, Leibnitz, Euler y otros. Intuitivamente lo reconocemos cuando queremos medir y representar las variaciones de ciertas magnitudes en dependencia de otras, por ejemplo la posición de un cuerpo en movimiento en función del tiempo o la presión dentro de una marmita en función de la temperatura. El nombre de función proviene de Leibnitz. El concepto de función es fundamental para el desarrollo y estudio de las matemáticas, en el cálculo diferencial e integral, las ecuaciones diferenciales y en todas sus aplicaciones en la Ciencia y la Tecnología.
Una función real f de una variable real, no es más que una regla que asigna a cada número x en un conjunto determinado de números, denominado el dominio de x, un solo valor de f(x). Al conjunto de los valores que toma f(x), se le denomina rango o dominio de imagen de la función f.
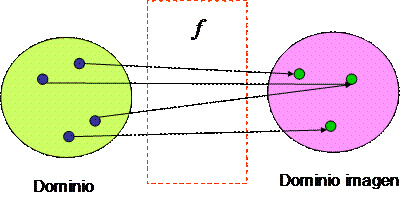
A continuación se exponen tres definiciones equivalentes de función:
1. F es una función entre 2 conjuntos A y B, sí y sólo sí F es una relación especial entre A y B de tal modo que todo elemento de A tiene un único correspondiente en B.
2. Una función F es el conjunto de pares ordenados de tal manera que la primera componente no se repite.
3. Una función F es el conjunto de pares ordenados en los cuales a cada elemento del Dominio le corresponde uno y sólo uno del rango.
Muchas veces escribiremos las funciones en la forma y = f(x) ; p = f(t); etc. En estos casos la variable y o la p se denominan variables dependientes y la x o la t se denominan variables independientes. Entonces podemos definir:
· Variable independiente: Es aquella cuyo universo está formado por las primeras componentes (x), de los pares ordenados (x,y) de una función (pudiéramos decir también cuyo universo es el dominio de la función).
· Variable dependiente: Es aquella cuyo universo está formado por las segundas componentes (y), de los pares ordenados de una función (pudiéramos decir también cuyo universo es el dominio de imagen de una función).
Ejemplos:
Halle el rango dado el dominio {2,4,6} de f(x) = 3x – 1
f(2) = 3(2) - 1 = 6 -1 = 5
f(4) = 3(4) - 1 = 12 - 1 = 11
f(6) = 3(6) - 1 = 18 - 1 = 17
El dominio imagen es {5,11,17} y los pares ordenados son (2,5); (4,11); (6,17)
Halle el dominio y rango de:

Como el denominador no puede ser igual a 0 el dominio es D = { x| x ¹ 3} y f(x) puede tener cualquier valor por tanto el rango es R = { f(x) | cualquier número real}
Una función puede ser especificada:
1. Numéricamente – mediante una tabla
2. Algebraicamente – por medio de una ecuación
3. Gráficamente – mediante una gráfica.
Numéricamente:
|
x |
0 |
1 |
2 |
3 |
|
f(x) |
3.01 |
-1.03 |
2.22 |
0.01 |
Entonces, f(0) = 3.01, f(1) = -1.03, y así sucesivamente.
Algebraicamente:
f(x) = 3x2 - 4x + 1. Entonces:
f(2) = 3(2)2 - 4(2) + 1 = 12 - 8 + 1 = 5,
f(-1) = 3(-1)2 - 4(-1) + 1 = 3 + 4 + 1 = 8.
Como f(x) está definida para toda x, el dominio de f es el conjunto de todos los números reales.
Gráficamente:

Entonces, f(0) = 1, f(1) = 0, and f(3) = 5.
El gráfico de una función es el conjunto de todos los pares ordenados (x,f(x)) en coordenadas cartesianas, donde restringimos los valores de x a los del dominio de f. Para que una gráfica sea la de una función dada, toda línea vertical debe intersecarse con la gráfica como máximo en un punto.
Ejemplo
Para obtener el gráfico de
f(x) = 3x2 - 4x + 1 (notación de función)
con domino restringido a (0, ¥), sustituimos f(x) por y obteniendo la ecuación:
y = 3x2 - 4x + 1 (notación de ecuación)
graficamos la misma situando los puntos o pares ordenados (x, y), estando restringida x a estar entre 0 e infinito y obtenemos:
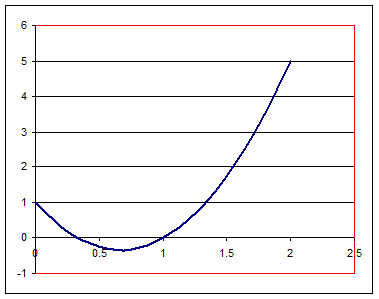
Las gráficas nos permiten identificar rápidamente si estamos en presencia de una función.
Prueba de la línea vertical:
Para comprobar si una gráfica corresponde a una función, trazamos una línea vertical y si esta se interseca con la gráfica en un solo punto es una función.
Prueba de la línea horizontal:
Si una línea horizontal intercepta a la gráfica en un solo punto esto indica que sólo hay un valor de f(x) asociado a cada valor de x. Estas funciones se denominan inyectivas o 1 a 1.
Ejemplo de aplicación de la prueba de la línea vertical:

Las gráficas de las funciones también nos permiten clasificarlas de acuerdo a como varían los valor de f(x) con x.
Siendo f(x) una función definida en el intervalo [a, b], f es creciente si y sólo si se cumple que estando x1 y x2 en el intervalo [a, b] y siendo x1 < x2 se tiene que f(x1) < f(x2). De manera similar la función es decreciente si f(x1) > f(x2). Una función f es monótona en [a, b] si y sólo si f es creciente ó decreciente en [a, b].Suma, substracción, multiplicación y división de funciones.
En general se cumple que:
( f + g )(x) = f(x) + g(x)
( f - g )(x) = f(x) - g(x)
( f · g )(x) = f(x) · g(x)
( f / g )(x) = f(x) / g(x)
En las anteriores operaciones, el dominio de la función resultante es la intersección de los dominios de f(x) y g(x), debiendo excluirse, en el caso del cociente, los valores que lo convierten en 0.
Ejemplo:
Dadas F(x) = 2x2, G(x) = x3, hallar la suma, diferencia, producto y cociente de las funciones.
(F+G)(x) = F(x)+G(x) = 2x2 + x3
(F- G)(x) = F(x) - G(x) = 2x2 - x3
(F.G)(x) = F(x).G(x) = 2x2.x3 = 2x5
(F/G)(x) = F(x)/G(x) = 2x2/x3 = 2/x
Composición de funciones.
En ocasiones es necesario aplicar una función al resultado de otra. Esto se denomina composición de funciones y se denota como gof que expresa en este caso que se tienen las funciones f(x) y g(x). Igualmente se puede plantear fog. Ilustremos esto con un ejemplo:
Sean:

Funciones inversas:
Para un par ordenado el inverso de (a,b) es (b,a).
Dos funciones son inversas si f(g(x)) = g(f(x)) = x
¿Cómo se hallan las funciones inversas?:
Ej. f(x) = 3x - 4
y = 3x - 4 sustituir f(x) por y
x = 3y - 4 sustituir x por y , y por x.
3y = x + 4 despejar y
y = (x+4)/3 sustituir y por g(x)
g(x) = (x+4)/3
La función inversa de 3x - 4 es (x+4)/3.
Ahora queda comprobar si se cumple la consideración f(g(x)) = g(f(x)) = x

O sea son efectivamente funciones inversas.
Gráfico de funciones inversas: Para hallar el gráfico de una función inversa se refleja la gráfica de la función en la línea y = x:
