Le invitamos a que repase de nuevo las propiedades de los exponentes, radicales y logaritmos. Es importante además que recuerde la definición de la función logaritmo con base a > 0 (con a ≠ 1):
![]()
La derivada de la función exponencial es igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente. En el caso que la base sea el número e evidentemente el logaritmo neperiano de la base es 1:
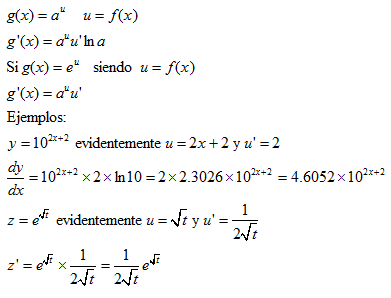
La derivada de un logaritmo de una función en base a es igual a la derivada de la función dividida por la función y por el logaritmo en base a de e. Utilizando la propiedad vista al principio, la derivada de un logaritmo de una función en base a es igual a la derivada de la función dividida por la función y dividida por el logaritmo en base e de a:
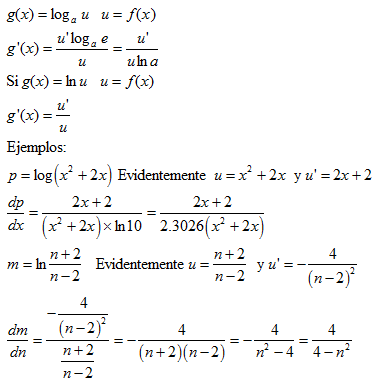
Enlace a material didáctico sobre derivadas de funciones exponenciales y logarítmicas.
Material de Khan Academy sobre derivación de funciones exponenciales y logarítmicas.