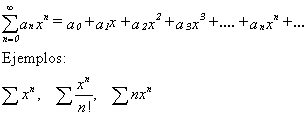
SERIES DE POTENCIAS
Una propiedad fundamental de las funciones analíticas es que pueden representarse por medio de series de potencias. También, salvo algunas excepciones toda serie de potencias convergente define una función analítica. Esto hace muy importante a las series de potencias para el estudio de funciones analíticas.
La expresión general de una serie de potencias es:
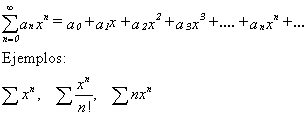
Sin pretender entrar en definiciones complejas diremos que las series pueden ser:
Convergente: Cuando la suma es un número real.
Divergente: Cuando la suma da + o - infinito.
Oscilante: Cuando no es ninguna de las anteriores.
En nuestro estudio nos interesan las series definidas alrededor de un punto:
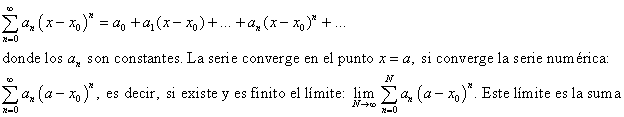
de la serie en x = a. En otro caso se dice que la serie diverge en x = a.
La serie puede converger para algunos valores de x y no para otros. Siempre converge para x = x0, siendo a0 su suma en dicho punto. El intervalo de x en que la serie converge I = (x0-R , x0+R) recibe el nombre de intervalo de convergencia de la serie y R el radio de convergencia de la misma. Si en particular R = 0 , se entiende que la serie converge únicamente para x = x0.
Para hallar el radio de convergencia se pueden utilizar el siguiente procedimiento:

Nótese que si l = 0, R = ¥ y si l = ¥ , R = 0
Por ejemplo, determinemos el radio de convergencia de la serie
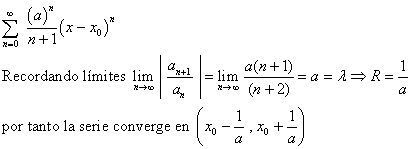
Se dice que una función f(x) es desarrollable en serie de potencias en un entorno de x0, si existe
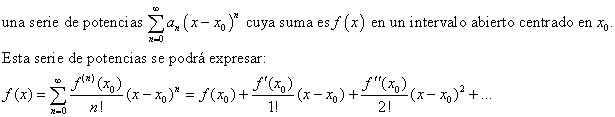
en un cierto intervalo abierto centrado en x0. Esta serie se llama serie de Taylor de f (x) en torno a x0. Si x0 = 0 , la serie se denomina serie de Maclaurin de f (x).
Veamos un ejemplo. Nos ceñiremos al desarrollo en x0 = 0. No obstante para x0 ≠ 0 basta hacer t = x – x0 y hacer el desarrollo para t.
Hallar la expresión de y = ex como una serie de potencias:
Del cálculo diferencial sabemos que y´ = y´´ = yn = ex, por tanto:
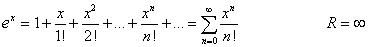
Ejercicios:
Hallar como series de potencias las siguientes funciones:
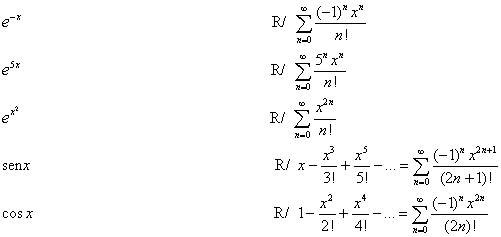
Una forma de expresar la serie de Taylor, que nos resulta importante, es aquella en la que consideramos el cambio de la función al variar de x a x+h, o sea cuando tenemos el incremento h en un punto. En ese caso:
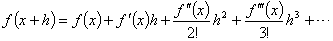
Siempre que existan todas las derivadas de f(x) y sean continuas en el intervalo x a x+h.
Por ejemplo:
Sea f(x) = sen(x). Determine el valor de sen(2) utilizando una serie de Taylor hasta la cuarta derivada..
R/
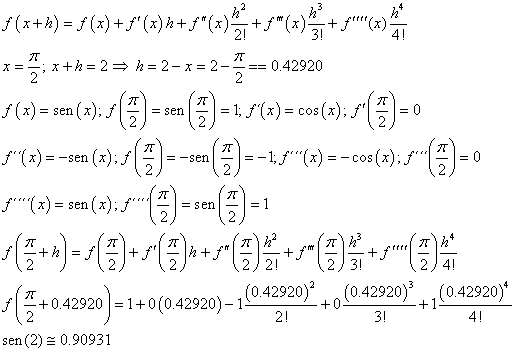
Nótese que entonces, si conocemos el valor de una función en un punto y los de sus derivadas en ese punto, podemos calcular el valor de la función en otro punto, con un grado de aproximación que dependerá de los términos de la serie de Taylor que tomemos.¿Qué error tendremos entonces? La expresión de la serie de Taylor donde se toman n términos, considerando el residuo Rn(x), es:
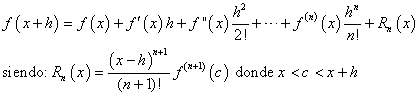
O sea c es un punto entre x y x+h.
En base a esta expresión podremos calcular los límites del error que se obtiene al truncar a n términos la serie de Taylor. Un ejemplo aclara. Hallemos el error producto de utilizar sólo los primeros 4 términos de la serie de Taylor para ex con h = 1.

Esto también nos permite determinar cuántos términos de la serie son necesarios para obtener u error determinado. Siguiendo en el mismo ejemplo de ex:
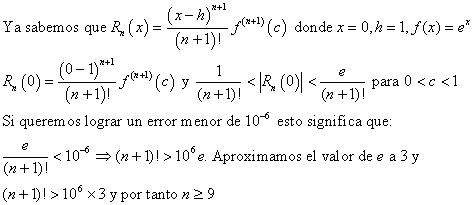
Entonces tendremos que utilizar hasta el 9 término de la serie para tener una diferencia menor a 10-6.
Les proporciono material auxiliar:
Unos apuntes sobre series de potencias que tienen ejemplos resueltos;
Una calculadora de series de potencias (puede tener anuncios, pero es útil), tiene su aplicación para series de Taylor;
Otra calculadora de series de potencias (también puede tener anuncios). Tiene ejemplos resueltos.