
Sólido de revolución
Un sólido de revolución es un cuerpo que puede obtenerse mediante una operación geométrica de rotación de una superficie plana alrededor de una recta que esté contenida en su mismo plano. Esto se ilustra en la siguiente animación (tomada de https://sites.google.com/site/calculo2meme/temas/solidos-en-revolucion-metodo-de-discos):

Por ejemplo: el cono es un sólido que resulta al girar un triángulo recto alrededor de uno de sus catetos; Una esfera al girar un semicírculo por su lado recto; el cilindro surge al girar un rectángulo alrededor de uno de sus lados, como se ilustra en la siguiente figura (tomada de http://profundizarenmatematicas.blogspot.mx/p/cuerpos-de-revolucion.html).

En principio, cualquier cuerpo con simetría axial o cilíndrica es un sólido de revolución
Volumen de los sólidos de revolución.
El volumen de los sólidos generados por revolución alrededor de los ejes cartesianos se puede obtener mediante las siguientes ecuaciones que contienen las integrales definidas.
Caso a. Rotación alrededor de un eje paralelo al eje de las abscisas:
Si se gira una figura plana comprendida entre y = f(x), y = 0, x = a y x = b alrededor del eje X, podemos irnos aproximando a la fórma requerida del sólido si generamos discos, cada vez más pequeños:
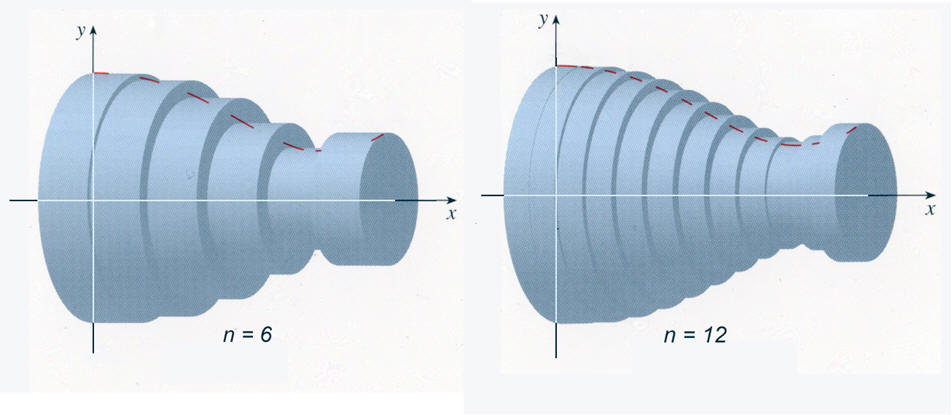
Entonces, cuando tomamos un gran número de discos, podemos considerar un disco infinitesimal y evaluar su volumen (ver la siguiente figura) que será evidentemente, en el límite cuando Dxi → dx, pf(x)2dx.
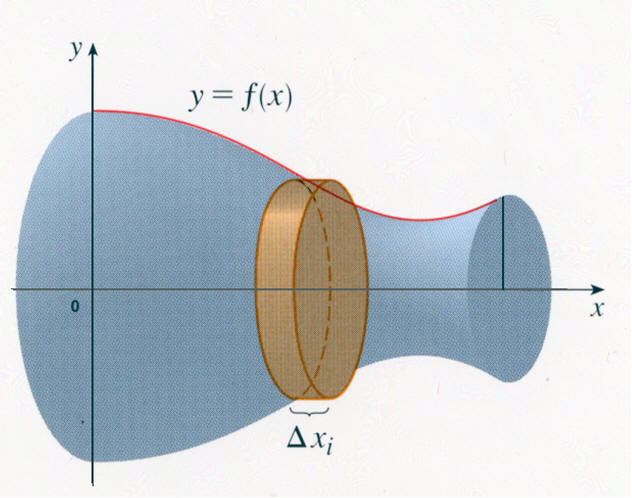
Si integramos en el intervalo [a, b], el volumen del sólido de revolución se obtiene por la fórmula:
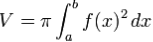
Lo anterior es conocido en esencia como el método de discos.
Para abundar más en el tema, pueden visitar una página sobnre el método de los discos.
En ocasiones, tenemos que hallar el volumen de sólidos huecos. En ese caso, tenemos que considerar dos volúmenes, el del exterior, dado por ejemplo por f(x) y el interior, dado por g(x). Esto equivale a considerar una arandela (imagen tomada de https://sites.google.com/site/calculo2meme/_/rsrc/1444327598424/temas/solidos-en-revolucion-metodo-de-arandelas/descarga.png):
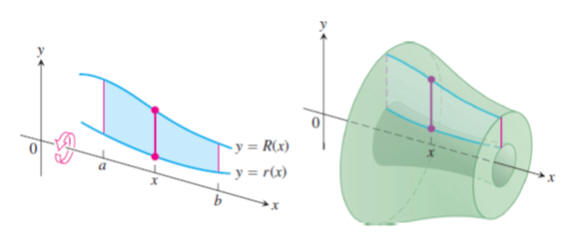
El volumen del corte Dx de la arandela será p[R(x)2 – r(x)2]Dx. En el límite, cuando Dxi → dx y tengamos la función exterior como f(x) y la interior como g(x), en el intervalo [a, b], podremos plantearnos la integral definida:
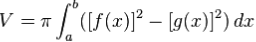
De manera general, el volumen de un sólido generado por el giro de un área comprendida entre dos gráficas, f(x) y g(x) definidas en un intervalo [a,b] alrededor de un eje horizontal, es decir, un recta paralela al eje X de expresión y = K siendo K constante, viene dado por la siguiente fórmula, que en casos extremos se reduce a las expresiones ya vistas:
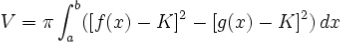
Pueden ver otros ejemplos en una página sobre el método de las arandelas.
Ejercicios para discutir y/o entregar: Del material del Profesor de España que se indica al final en la Página 3, Ejemplo 4, los incisos a, c, d y f; Página 4, Ejemplo 5, incisos a y b.
Ver una página de la UNAM sobre los sólidos de revolución y revisar los ejemplos.
Caso b. Rotación alrededor de un eje paralelo al eje de ordenadas:
Si el sólido de revolución es generado por el giro de un área comprendida entre dos funciones, f(x) y g(x), en un intervalo [a,b] alrededor de un eje paralelo al eje de ordenadas cuya expresión es x = K siendo K constante. La fórmula general del volumen de estos sólidos es:
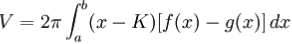
Que para el caso de un área comprendida entre y=f(x), y=0, x=a y x=b alrededor del eje Y, el volumen del sólido de revolución viene dado por:
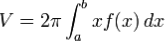
Método de las capas.
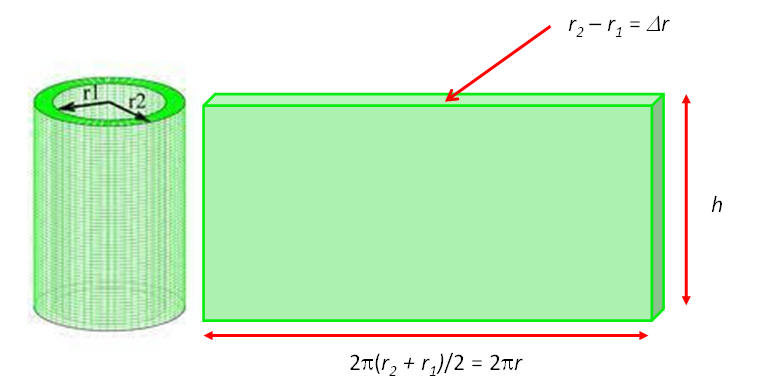
Hay otro método, que se utiliza cuándo al rotar se obtiene un sólido hueco, pero sólo disponemos de un radio. Si desenrollamos una capa, como se muestra en la figura que sigue, obtenemos para el volumen del paralelepípedo así obtenido la fórmula V = 2prDr.
Un ejemplo se muestra en la siguiente animación (tomada de http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Links/aplicaciones_integral_lnk_7.html), para el cálculo del volumen de un sólido y se observa cómo al aumentar el número de divisiones del intervalo se mejora la resolución de la figura.
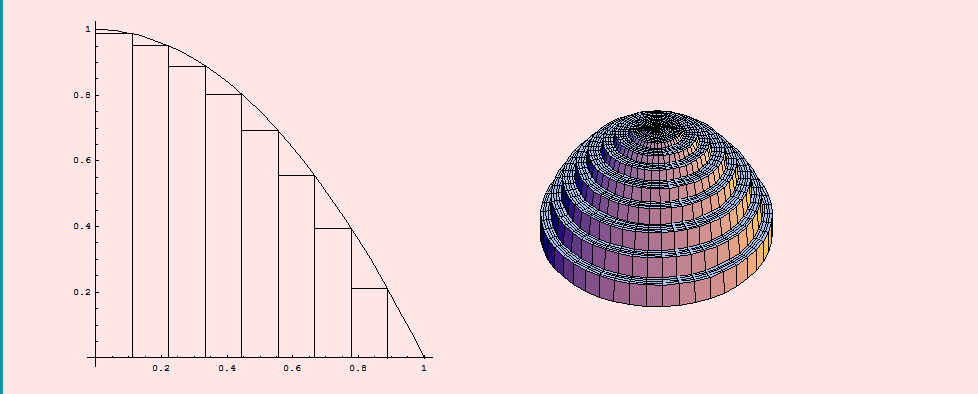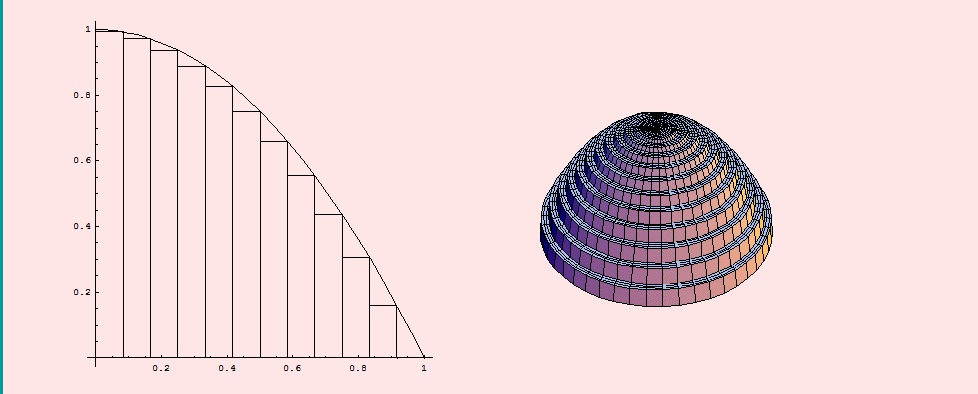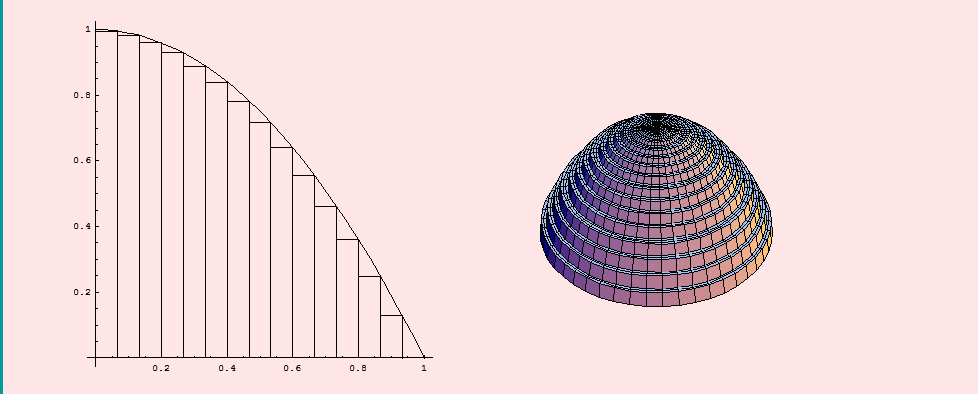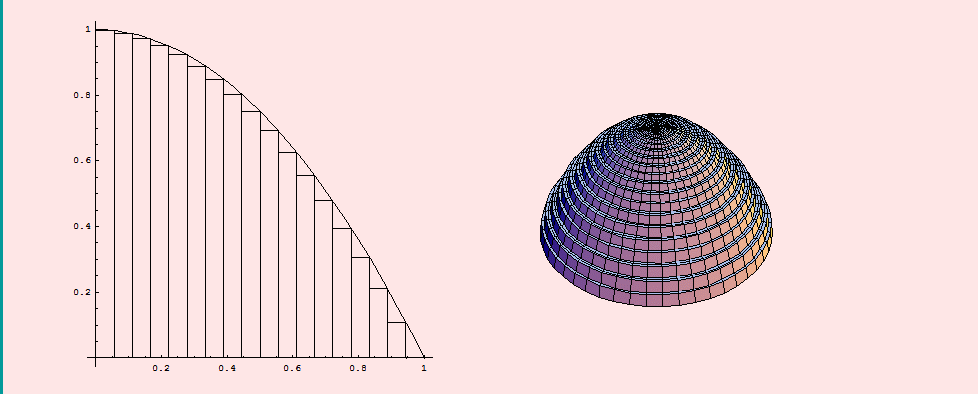
En el límite esta fórmula puede ser extrapolada a la forma de una integral definida como:
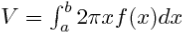
Otras animaciones que me resultaron interesantes para ilustrar el método de las capas están en la página http://tornadoscalculointegral.blogspot.mx/, que muestra la idea del cálculo de un tornado:
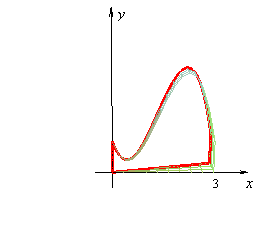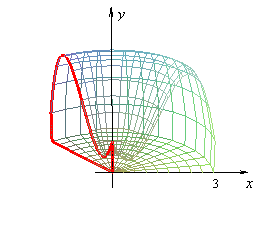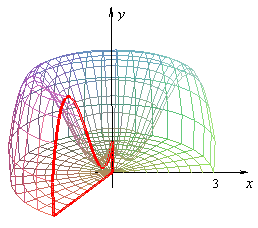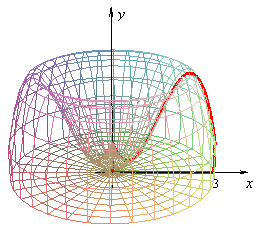
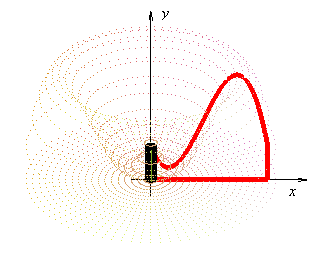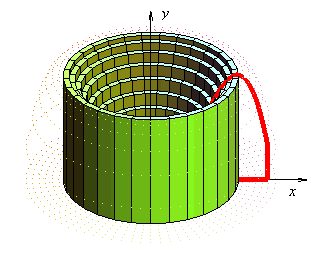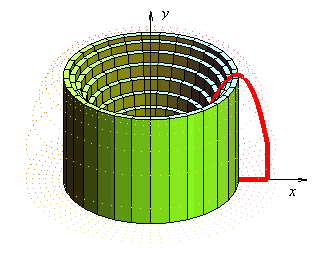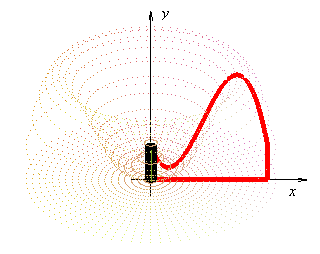
Pueden ver ejercicios resueltos paso a paso en una página de ekuatio.com, aunque tiene anuncios.
Para abundar en este método pueden acceder a una página sobre el método de las capas.
Ejercicios para discutir y/o entregar: Del material del Profesor de España, Página 7, Ejemplo 7. incisos a y b.
Aquí les dejo ejercicios de aplicación de las integrales definidas (incluyendo de los sólidos de revolución), unos de un profesor de España y los otros de un Profesor de Ecuador.