Distribuciones continuas

Al considerar las variables continuas se encuentra uno el problema de que, lo más probable, los datos que se colectan no sean completamente exactos, o que muchos de ellos no coincidan, por lo que se tiene que trabajar en intervalos siendo complicado modelar los datos de acuerdo a una función que se elabore. Sin embargo, se pueden realizar aproximaciones y describir la probabilidad asociada a los valores de la variable aleatoria utilizando de modelos teóricos de probabilidad cuya gráfica es una línea continua, a diferencia de las variables discretas, a las que corresponde un histograma. Esta línea continua es la gráfica de una cierta función que ya vimos que denominamos función de densidad de probabilidad.

Modelos de distribución de probabilidad de variables continuas

Al igual que en el caso de las distribuciones de probabilidad de variables discreta, en el caso de las distribuciones de probabilidad de variables continuas se tienen varios modelos:

• Uniforme. Es la distribución en donde todos los eventos tienen la misma probabilidad.

• Exponencial. Se utiliza para estudiar el tiempo entre dos sucesos.

• Beta. Sirve para el estudio de variaciones, a través de varias muestras, de un porcentaje que representa algún fenómeno.

• Gamma. Se utiliza para estudiar variables cuya distribución puede ser asimétrica.

• Ji cuadrada (ξ²). Es una distribución asociada a la prueba ξ², y se usa para comparar los valores observados con los esperados.

• Normal. Es la distribución más utilizada porque muchas de las variables utilizadas en fenómenos de la ingeniería se distribuyen aproximadamente siguiendo este modelo. Es la que abordaremos a continuación y se le llama comúnmente distribución normal.

La distribución normal

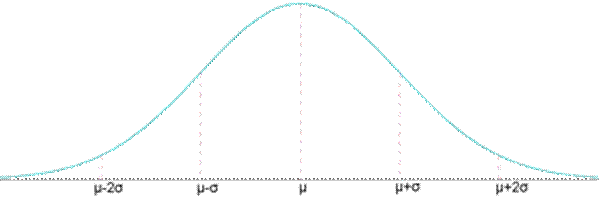
Es el modelo de distribución más utilizado en la práctica, ya que multitud de fenómenos se comportan según una distribución normal. Se caracteriza porque los valores se distribuyen formando una campana de Gauss, en torno a un valor central que coincide con el valor medio de la distribución:

Un 50% de los valores están a la derecha de este valor central y otro 50% a la izquierda.

Esta distribución viene definida por dos parámetros: X: N (m, s²):

m: es el valor medio de la distribución y es precisamente donde se sitúa el centro de la curva (de la campana de Gauss).

s²: es la varianza. Indica si los valores están más o menos alejados del valor central: si la varianza es baja los valores están próximos a la media; si es alta, entonces los valores están muy dispersos.

Cuando la media de la distribución es 0 y la varianza es 1, se denomina "normal tipificada", y su ventaja reside en que hay tablas donde se recoge la probabilidad acumulada para cada punto de la curva de esta distribución. Toda distribución normal se puede transformar en una normal tipificada. Por ejemplo, una variable aleatoria sigue el modelo de una distribución normal con media 10 y varianza 4. Transformarla en una normal tipificada.

X: N (10, 4)

Para transformarla en una normal tipificada se crea una nueva variable (Y) que será igual a la anterior (X) menos su media y dividida por su desviación típica (que es la raíz cuadrada de la varianza):

Esta nueva variable se distribuye como una normal tipificada, permitiéndonos, por tanto, conocer la probabilidad acumulada en cada valor Y: N (0, 1).

Propiedades de la curva de distribución normal

Las propiedades de la curva son básicamente seis, y su demostración está basada en conceptos de cálculo que no veremos ahora:

1. Los valores de la curva son positivos.
2. La curva es simétrica con respecto al valor de la media.
3. La curva tiene un valor máximo en el valor de la media.
4. La curva tiene puntos de inflexión en aquellos valores de x para los cuales a la media se le suma o se le resta una desviación estándar.
5. La curva, en sus extremos izquierdo y derecho, tiende a acercarse infinitamente al valor cero, es decir, el eje de las abscisas es asíntota horizontal.
6. El área bajo la curva es la unidad.

La distribución normal tipificada tiene la ventaja, como ya hemos mencionado, de que las probabilidades para cada valor de la curva se encuentran recogidas en una tabla.

¿Cómo utilizar la tabla?

La columna de la izquierda indica el valor cuya probabilidad acumulada queremos conocer. La primera fila nos indica el segundo decimal del valor que estamos consultando.

Ejemplo: queremos conocer la probabilidad acumulada en el valor 2.75. Entonces buscamos en la columna de la izquierda el valor 2.7 y en la primera fila el valor 0.05. La casilla en la que se intersectan es su probabilidad acumulada (0,99702, es decir 99.7%).

Para calcular los valores negativos de Z, uno se basa en la simetría de la función de distribución normal. Por ejemplo la probabilidad acumulada hasta Z = -0,5 es igual 1 menos la probabilidad hasta 0.5:

P(Z£-0.5) = 1- P(Z£0.5)

Nota: Recordar que la tabla nos da la probabilidad acumulada, es decir, la que va desde el inicio de la curva por la izquierda hasta dicho valor. No nos da la probabilidad concreta en ese punto. En una distribución continua en el que la variable puede tomar infinitos valores, la probabilidad en un punto concreto es 0. Recuerden que se trabaja con probabilidades en intervalos. Para hallar los valores que corresponden a determinada probabilidad, se usa la interpolación lineal.

Si no se dispone de un paqute estadístico, el cálculo de las probabilidades se puede hacer con una calculadora en línea, por ejemplo, la disponible en este vínculo. Una sencilla está disponible en una página de la Universidad de Granada.

Ejercicio:

Busque en la tabla las probabilidades acumuladas hasta los valores 0.71, 1.83, 2.25

Halle los valores de X que corresponden a probabilidades acumuladas de 0.75, 0.80, 0.90 y 0.95.

Para ampliar en este tema puede consultar algunos aspectos teóricos en una página de Khan Academy y ver algunos ejemplos resueltos en otra página.

Aplicaciones de la distribución normal.

Veamos esto a través de 1 ejemplo.

El contenido de grasa en un alimento se distribuye según una distribución normal con media 5 % y desviación estándar de 1. Determinar, en un lote de 1200 unidades:

A) el número de unidades con un contenido de grasa inferior a 6.5 %;

B) el número de unidades con un contenido de grasa inferior a 4 %;

C) el porcentaje de grasa por debajo del cual está el 5% de las unidades.

Sea g el contenido de grasa. Transformemos la distribución en una normal tipificada haciendo el cambio de variable G = (g – m)/s = (g – 5)/1

A) La variable G que corresponde a una variable g de valor 6.5 es: G = (6.5 – 5)/1 = 1.5

En la tabla la probabilidad acumulada para el valor 1.5 (equivalente a la probabilidad de un contenido de grasa inferior a 6.5%), es 0,9332. Esto indica que el porcentaje de unidades con un contenido de grasa inferior a 6.5 % es del 93.32, entonces el número de unidades es igual a 0.9332*1200 = 1119 unidades

B) La variable G que corresponde a una variable g de valor 4 es: G = (4 – 5)/1 = - 1.

Haciendo uso de la simetría P(X£-1) = 1 – P(X£1) = 1 – 0.8416 = 0.1584 y el número de unidades que tienen grasa inferior a 4 % es 0.1584*1200 = 190 unidades.

C) De acuerdo a la simetría de la curva, el valor del 0.05 corresponde al valor de G que corresponde a 0.95 con el signo cambiado. Buscando en la tabla, el valor de 0.95 corresponde a G = 1.645, por tanto el valor de G para el cual la probabilidad es 0.05 es -1.645. Entonces: -1.645 = (g – 5)/1 de donde g = 5 -1.645 =3.355, o sea el 5 % de las unidades tiene un porcentaje de grasa inferior a 3.355.

Ejercicios para discutir en el salón:

Después de una selección, el peso de las papayas en una empacadora de frutas se distribuye según una Normal de media 600 g y desviación típica 100 g.. Hallar la probabilidad de que al elegir al azar una papaya su peso sea:

·    Mayor de 750 g.

·    Menor de 700 g

·    Esté comprendido entre 500 y 800 g

·    Igual a 600 g

El contenido de un conservador, en mg, se distribuye en un alimento según una distribución normal N(1,85, 0.20). Hallar la probabilidad de que al elegir al azar una unidad, el contenido del conservador sea:

Mayor de 2,05 mg

Menor de 1,75 mg

Esté comprendido entre 1,75 y 1.95 mg

Diga los valores de contenido de conservador a los cuales corresponden los porcentajes de 2.5 y 97.5 % de las unidades.

Tarea 2: Resuelva los siguientes ejercicios. Indicar el resultado pero ilustrando o argumentando su respuesta.

1. Para un producto se recomienda un contenido de grasa menor al 7%, un contenido de proteína >5% y un contenido de fibra >3%. Representando por G, P y F el cumplimiento de lo especificado, se encuentra en un lote de productos que 68 cumplen F, 160 cumplen P, 138 cumplen G, 55 cumplen P y F, 48 cumplen F y G, 120 cumplen P y G y 40 cumplen los tres requisitos. ¿Cuál es el número de productos que solamente cumplen con el % de grasa?

2. Obtenga todos los números diferentes de tres cifras que se pueden obtener con los dígitos 2, 4, 5, 8 con la condición que ninguno se repita. Escriba todos esos números.

3. En una industria se tienen los siguientes componentes para fabricar un alimento: 4 concentrados vitamínicos, 3 tipos de aditivos antioxidantes y 2 tipos de colorantes. Determine con un diagrama de árbol los posibles productos finales.

4. Se dispone de la posibilidad de emplear 2 componentes, para mejorar las propiedades y textura de un alimento, pudiéndose seleccionar de entre 5 productos. Determine el número de posibilidades si: a) es importante el orden en que se añaden b) no importa el orden en que se añaden.

5. Determine la probabilidad de que al entrar 5 clientes a una tienda, al menos 2 compren un producto que, según una encuesta, tiene una aceptación del 40 %. Grafique el histograma correspondiente y haga la comparación co el que se obtiene si la aceptación del producto es de un 60 %.

6. Sea X una variable aleatoria que representa el peso medio de aditivo, en mg, suministrado por un dosificador. Si X es N(100, 10), obtener las probabilidades de que X sea mayor que 100, menor que 85, a lo más 110, por lo menos 108, más grande que 90 y entre 95 y 120.

7. Si la demanda mensual de cierto producto se encuentra aproximada por una variable X N(200, 40) ¿ Qué tan grande debe ser el inventario disponible a principio de un mes para que la probabilidad de que la existencia se agote no se mayor de 0.05?

REGRESAR