
Derivadas Parciales y Vectores
El gradiente de una función
Formalicemos un poco un concepto que Ustedes tienen de sus estudios previos, el concepto de Operador Matemático. Si escribo:

Estoy seguro que interpretan que estamos derivando la función F(x) con respecto a x. Precisamente d/dx nos ilustra lo que es un operador matemático. Podemos definirlo como un símbolo que actúa sobre otro símbolo (puede ser un número una función de magnitudes escalares, un vector), dando como resultado otro símbolo. Esta acción es una operación.
Definamos entonces el siguiente operador, al que llamaremos operador nabla:

Como ya mencionamos anteriormente, si a cada punto en una región dada de R3 le asignamos un valor numérico determinado por una función, digamos j(x,y,z), o sea un escalar, tenemos un campo escalar. Ya vimos también que las superficies de nivel en general son aquellas en las que j(x,y,z) = constante (recuerden que en dos dimensiones tendríamos curvas de nivel) y cualquier desplazamiento en esa superficie tiene dj = 0 o sea dj = jx . dx + jy . dy + jz . dz = 0 lo que nos indica que el gradiente es normal a cualquier desplazamiento sobre una superficie de nivel, pues su producto escalar por el vector desplazamiento es nulo.
Se llaman lineas de gradiente de un campo escalar j a las que en cada punto tienen la tangente en la dirección del gradiente de j. Esto significa que la dirección del gradiente coincide en cada punto con la del desplazamiento sobre la curva o sea

Para obtener la expresión del gradiente en otras coordenadas se aplica la regla de la cadena y se toman en cuenta las expresiones de los vectores unitarios en función de los vectores unitarios en coordenadas cartesianas. El interesado puede hacer la deducción.
En coordenadas cilíndricas:

Estas expresiones se utilizarán cuando sea necesario y las deben incorporar al formulario de la asignatura.
Veamos dos ejemplos.
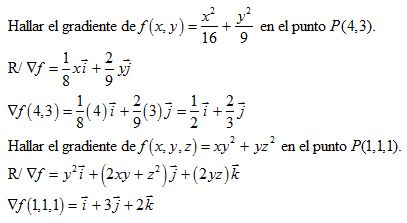
Si definimos un vector unitario u en la dirección en que nos interesa evaluar la rapidez de cambio de una función f, o sea la derivada direccional Du, esta será:
![]()
Esta es una forma sencilla de calcular la derivada direccional.
Ya estamos entonces en condiciones de poder evaluar la derivada de una función de varias variables en cualquier dirección del espacio.
Ejemplo: Si f(x,y) = 3x2 – 2y2, hallar la derivada direccional en el punto (-1,3) en la dirección del vector que va de (-1,3) a (1,-2).
R/ El vector que va de (-1,3) a (1,-2) lo hallamos restando las coordenadas:

El gradiente nos va a permitir evaluar para una función:
El valor de crecimiento máximo |Ñf | cuando u y Ñf tienen la misma dirección.
El valor de crecimiento mínimo – |Ñf | cuando u y Ñf tienen dirección opuesta.
Veamos un ejemplo clásico tomado de Internet.
La temperatura en °C sobre la superficie de una placa metálica viene dada por la función f(x,y) = 20 - 4x2 – y2, midiéndose x e y en pulgadas, desde el punto (2,-3).
a) ¿En que dirección crece la temperatura más rápidamente?
b) ¿Cuál es su valor de crecimiento máximo?
c) ¿En que dirección decrece la temperatura?
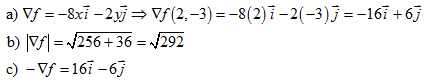
Otro ejemplo:
Calcular la derivada direccional y el valor de crecimiento máximo de f(x,y)= x2e2yz en el P(-1,0,2), en la dirección del vector que va de (-1,0,2) a (1,3,-2).
R/

Enlace a un material sobre el gradiente de una función.
Les enlazo a un material sobre la derivada direccional y el gradiente que éstá interesante, les permitirá ampliar y que tiene ejercicios resueltos.
Para ver bien ilustrados ambos conceptos, pueden ver un material de libretexts.
Pueden acceder a un video sobre la derivada direccional y el gradiente