Integrales de línea

Integrales de línea

El último tema que vamos a abordar es el de las integrales de línea. Es un tema que presenta determinada complejidad y por lo cual no vamos a repetir la información que otros docentes o colectivos de docentes ya han elaborado. Por ello vamos a ceñirnos a definir la integral de línea y a abordar la solución de algunos ejemplos.

Para ampliar este tema les enlazo a:

Una página de OpenStax que encontré interesante.

Página web de Khan Academy, tanto en campos escalares como en campos vectoriales;

Un material de un profesor de la Universidad de San Luis Potosí.

La importancia de este tema radica en que hay casos en los que nos interesa evaluar una función sobre una trayectoria dada en el espacio (en su sentido más general, no sólo el espacio físico tridimensional en el que nos encontramos), o sea sobre una curva. Por ejemplo, como ya se vió, calcular la longitud de una curva en el espacio. Nos puede interesar, por ejemplo, calcular las cantidades de calor que le serán transmitidas a un cuerpo durante su tránsito por una placa plana en la cual, para cada punto en el plano x,y tenemos un valor de la temperatura. Este caso es el típico de un ampo escalar, que es aquel para el cual, para cada punto hay un valor de una variable numérica. También, nos puede interesar el trabajo que habrá que realizar al mover un objeto una distancia, por una trayectoria determinada para la cual en cada punto tenemos un valor determinado de un campo de fuerzas. Este es un ejemplo típico de un campo vectorial.

Les vinculo un material con ejemplos que pueden ilustrarles más en las aplicaciones. está en inglés, pero eso les ayudará en s formación integral. También hay algunos ejercicios con su respuesta en una página del Whitman College (USA), que les vinculo, también en inglés.

Como ya se vió, en forma vectorial y parametrizada yo puedo representar una curva en el espacio como:

y su longitud (por ejemplo para dos dimensiones):

Integrales de línea en campos escalares.

Partiendo de lo anterior, podemos entender la definición de la integral de línea a través de las siguientes ecuaciones equivalentes y que utilizaremos para el cálculo de las integrales

El sentido de la integración es importante y se considera que integrar en sentido contrario a las manecillas del reloj es positivo. Si se hace en sentido contrario, se multiplica por -1.

Veamos unos ejemplos sencillos, tomados de una página de un profesor de la Universidad de Lamar.

Evaluar la integral de línea:

Siendo C la parte derecha del círculo

rotando en sentido contrario a las manecillas del reloj.

Lo primero es parametrizar el círculo, lo que viene dado por:

Lo segundo es determinar los límites inferior y superior que nos darán la primera mitad del círculo, lo que evidentemente será

Entonces necesitamos derivar la ecuación paramétrica y hallar ds:

Y la integral de línea será:

Veamos otro ejemplo, con los valores de las integrales en x y y:

Evaluar la integral

Siendo C el segmento de recta de (0,2) a (1,4).

respuesta

La parametrización de la curva será:

Y la integral de línea es:

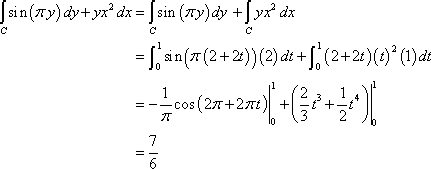
Veamos que significa cambiar el sentido del recorrido por la curva, evaluando la misma integral pero siendo C el segmento de recta de (1,4) a (0,2). La nueva parametrización será:

Y la integral de línea será:

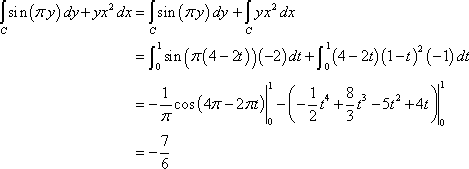
Integrales de línea en campos vectoriales.

Cuando consideramos un campo vectorial, asociamos que a cada punto del espacio le corresponde un valor de un vector, digamos por ejemplo, un campo magnético en el analizador de un espectrómetro de masas. Entonces: