.
SUSTANCIAS PURAS
Gases ideales y reales
Gas ideal.
La mayoría de las sustancias pueden existir como gases, líquidos o sólidos, dependiendo de las condiciones de presión y temperatura. Existen como gases a condiciones normales de presión y temperatura ( 1 atm y 25 ºC) los elementos N, O, F, Cl y H como moléculas biatómicas y los gases nobles como moléculas monoatómicas. En condiciones normales existen como gases muchos compuestos como amoníaco, monóxido de carbono, dióxido dc carbono, halogenuros de hidrógeno, monóxido y dióxido de nitrógeno, dióxido dc azufre, sulfuro de hidrógeno, etc.
Gas ideal es un gas cuyas moléculas no se atraen ni repelen entre sí y cuyas distancias intermoleculares son muy grandes.
Al igual que en la mayoría de los campos de la ciencia, la generaliación en una sola ley de las propiedades de los gases, se dio a través del estudio y deducción de leyes particulares.
Ley de Boyle:
Si fijamos la cantidad de gas y su temperatura, pero modificamos la presión a la que se halla sometido, veremos qué cuanto mayor sea la presión, menor será el volumen que ocupe. El físico inglés Robert Boyle y el francés Edme Mariotte, trabajando independientemente uno de otro descubrieron la relación numérica entre la presión y el volumen de un gas: Si no varía la temperatura a la que se encuentra un gas, el producto del volumen que ocupa por la presión que ejerce es constante. Matemáticamente, la ley de Boyle-Mariotte puede enunciarse P0*V0=P1*V1en la que los subíndices 0 indican la presión y volumen inicial y los subíndices 1 la presión y el volumen después.
Ejemplo: El globo de un niño se ha inflado con helio, hasta alcanzar un volumen de 3 l, a la presión de 760 mmHg. Se le escapa al niño subiendo hasta una altura en la que la presión es de 0.9 bares. ¿Qué volumen tiene el globo?
En primer lugar deberemos expresar la presión en las mismas unidades de medida: como 1.013 bar son 760 mmHg, 0.9 bares serán
.
Ahora se puede aplicar la ley de Boyle-Mariotte: P0*V0=P1*V1,
siendo P0 = 760 mmHg, V0
= 3 l y P1 = 675.22 mmHg, quedando 
,
multiplicando 760 por 3: 2280 = 675.22V1, y como 675.22 está
multiplicando, pasa al otro miembro de la ecuación dividiendo: 
,
por lo que el volumen resulta: 3.377 l.
Ley de Charles y de Charles – Gay-Lussac
En 1787, Jacques Charles, químico francés que fabricó el primer globo de hidrógeno, y años más tarde Joseph Gay-Lussac, también francés, estudiaron la relación existente entre el volumen de un gas y su temperatura. Al aumentar la temperatura aumenta el volumen, pero si la temperatura se expresa en la escala Kelvin o absoluta, la temperatura y el volumen son directamente proporcionales (al duplicar una, se duplica la otra, al multiplicar una por 3, otro tanto le sucede a la segunda). Siguiendo la notación de la ley de Boyle-Mariotte, podemos escribir:
donde el subíndice 0 indica el volumen y la temperatura iniciales del gas y el subíndice 1 los valores finales de volumen y temperatura: cuando la presión no varía, el cociente entre el volumen ocupado por un gas y la temperatura a la que se encuentra, permanece constante. Es preciso señalar que los volúmenes pueden ser medidos en cualquier unidad, siempre que coincidan ambos, pero la temperatura debe expresarse en la escala Kelvin.
La misma relación existe entre la presión y la temperatura de un gas:
.
Cuando el volumen no cambia, el cociente entre la presión de un gas y su temperatura permanece constante.
Ejemplo: Si el volumen del aire de una habitación a 10 ºC es de 90000 l, ¿cuánto aire escapará de la habitación si se calienta hasta 30ºC?
En primer lugar debemos expresar las temperaturas en Kelvin, es
decir debemos sumarle 273 a cada una de ellas. Así la temperatura inicial T0
será 10 + 273 = 283 K y la final, T1, valdrá 273 + 30 = 303 K. Como
el volumen inicial es de 90000 litros, aplicando la ley de Charles
obtendría:
realizando la división del primer miembro de la ecuación quedará 
.
Como 303 está dividiendo, pasará multiplicando: 
,
con lo que el volumen final será de 96360,42 litros. La cantidad de aire que
saldrá de la habitación será de 96360,42 -90000 = 6360.42 litros.
Ejemplo: A 20 ºC, la presión del neumático de un coche es de 1.8 atm. Tras recorrer 50 km la temperatura del neumático es de 60 ºC, ¿cuánto valdrá su presión?
Debemos, en primer lugar, expresar las temperaturas en
Kelvin, por lo que añadimos 273 a cada una de ellas, quedando T0
= 293 K y T1 = 333 K. Aplicando ahora la relación entre presión y
temperatura: 
.
Multiplicando en cruz, para eliminar los denominadores obtendríamos
.
Al multiplicar quedaría 599,4 = 293P1, y pasando 293 dividiendo, la
presión deseada es de 2.05 atm.
Gracias a las leyes de Boyle-Mariotte y de Charles y Gay-Lussac, conocemos las relaciones que hay entre la presión, el volumen y la temperatura de un gas, pero siempre que una de las tres permanezca constante. Intentaremos determinar que ocurre cuando cambiamos las tres propiedades, presión, volumen y temperatura, simultáneamente. ¿Qué pasa al cambiar las tres variables.
Digamos que las condiciones iniciales del gas son P0, V0 y T0, y las finales P1, V1 y T1. Podemos suponer que en un principio cambiamos sólo el volumen y la presión, dejando constante la temperatura. El gas, pasaría de las condiciones iniciales P0, V0 y T0 a las finales P1, V1 y T0. Ahora cambiaríamos únicamente el volumen y la temperatura, de forma que el gas pasaría de estar P1, V' y T0 a P1, V1 y T1.
En el primer cambio, como no cambia la temperatura, se cumple la ley de
Boyle-Mariotte, es decir, el producto de la presión y el volumen es
constante: P0 x V0 = P1 x V1. En el segundo
caso se cumple la ley de Charles y Gay-Lussac, el cociente
entre volumen y temperatura es constante: V0/T0 = V1/T1.
Como en las dos ecuaciones que obtengo aparece el término V', puedo despejarlo
en la segunda y sustituirlo en la primera obteniendo la ecuación:
y agrupando según el subíndice quedará:
que es la Ley de los gases: el producto de la presión y el volumen de un gas, dividido por la temperatura a la que se encuentra permanece siempre constante. Como en la ley de Charles y Gay-Lussac, la temperatura ha de estar expresada en Kelvin.
Ejemplo: Los neumáticos de un coche deben estar, a 20 ºC, a una presión de 1'8 atm. Con el movimiento, se calientan hasta 50 ºC, pasando su volumen de 50 a 50.5 litros. ¿Cuál será la presión del neumático tras la marcha?
En primer lugar debemos expresar las temperaturas en Kelvin, es
decir debemos sumar 273 a cada una de ellas. Así la temperatura inicial T0
será 20 + 273 = 293 K y la final, T1, valdrá 273 + 50 = 323 K, como
el volumen inicial es de V0 = 50 litros y el final de V1 =
50.5 litros y la presión inicial P0 = 1.8 atm, aplicando la
ley de los gases obtendremos: 
realizando
las operaciones del primer miembro de la ecuación quedará 
.
Como 323 está dividiendo, pasará multiplicando y 50.5 que multiplica, pasará
dividiendo: 
,
con lo que la presión final será de 1'965 atm.
Ejemplo: Cierto gas ocupa un volumen de 5 l a 20 ºC y una presión de760 mmHg. Si se comprime hasta 2500 cc a 1'2 atm, ¿cuánto valdrá su temperatura?
Debemos, en primer lugar, expresar la temperatura en Kelvin,
por lo que añadimos 273 a 20 ºC quedando 293 K. Las presiones deben expresarse
en la misma unidad, así que como P0 = 760 mmHg, expresaremos P1
en mmHg, para lo que multiplicamos por 760 (760 mmHg es lo mismo que 1 atm),
quedando P1 = 912 mmHg. Otro tanto ocurre con los volúmenes, como V0
= 5 l, tenemos que poner V1 en litros también. 2500 cc equivalen a
2'5 dm3 (al ser cúbico, debemos dividir entre mil), que son 2'5 l. Aplicando
ahora la ecuación de los gases: 
.
Realizando las operaciones quedará 
.
Como T1 está dividiendo, pasará multiplicando al primer miembro de la
ecuación 12.969xT1=2280, y pasando el número que multiplica a la
temperatura dividiendo nos quedará que ésta es de 175.80 K o -97.20 ºC.
Ley de Avogadro:
A temperatura y presión constante, el volumen de un gas es proporcional al número de moles del mismo. Un mol de cualquier gas a temperatura 0 ºC y 1 atm de presión ocupa 22.4 L.
Simulación de las leyes de los gases:
Este vínculo le llevará a una ilustrativa simulación que muestra la relación entre P, V, T y n, con sus gráficas correspondientes. Debe disponer de internet.
Igualmente puede ver otra simulación de PHET, que ilustra estas relaciones.
La ecuación de los gases ideales.
Ya hemos visto que el volumen de un gas depende de la temperatura y la presión a la que se encuentra, de forma que al aumentar la temperatura aumentará su volumen (ley de Charles y Gay-Lussac) y al aumentar la presión el volumen disminuirá (ley de Boyle-Mariotte). Está claro que también dependerá de la cantidad de gas que tengamos: si aumentamos la cantidad de gas, debe aumentar su volumen.
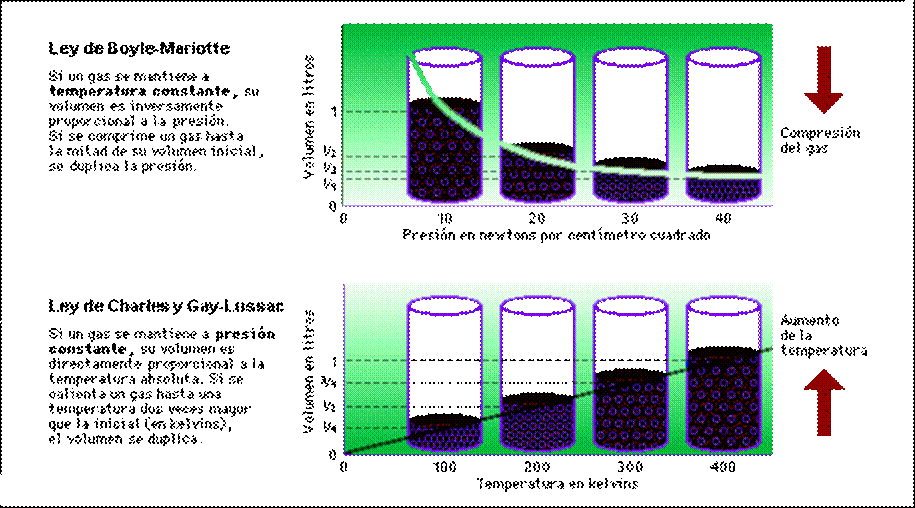
Pero la cantidad de gas que influye no es su masa, sino las moléculas de gas presentes: el número de moles: un mol de gas a 0 ºC y una atmósfera de presión ocupa siempre 22'4 litros, dos moles 44'8 litros etc. Por la ley de los gases sabemos que:
Si tenemos un mol de gas a 0 ºC (273 K) y 1 atmósfera de presión, ocupa siempre 22'4 l, por lo que sustituyendo en la ecuación anterior nos queda:
Ese número se denomina constante de los gases ideales y se designa por
la letra R. Podemos escribir entonces: 
y
pasando T al otro miembro de la igualdad 
.
Y, si indicamos por n el número de moles: 
.
Ecuación esta última que se conoce como ecuación de los gases ideales.
Ejemplo: ¿Qué volumen ocuparán 3 moles de gas a 300 K y 2 atm de presión?
Sustituyendo en la ecuación de los gases ideales 
,
quedará la ecuación: 2*V = 3*0.082*300, ya que R vale 0.082. Multiplicando en el
segundo miembro de la igualdad quedará 2*V = 73.8, y pasando el 2 dividiendo: V
= 31.9 litros.
Ejemplo: ¿Cuántos moles de gas serán necesarios para que a 27 ºC y 2 atm ocupen un volumen de 22.4 litros.
En primer lugar habremos de pasar la temperatura a Kelvin, sumando 273: T=27+273=300 K. Podemos ya sustituir en la ecuación de los gases ideales: 22.4*2=n*0.082*300. Multiplicando en ambos miembros quedará 44.8=24.6*n, y pasando 24.6 dividiendo, n=1.82 moles.
Está disponible una calculadora para los gases ideales (cita de la página: Generalic, Eni. "Calculadora con leyes de los gases." EniG. Tabla periódica de los elementos. KTF-Split, 3 Mar. 2020. Web. 3 May. 2020. <https://www.periodni.com/es/calculadora_con_leyes_de_gases.html>). También hay una calculadora para móvil (Ideal Gas Calculator de slh.dzdev en Google PLay. Esto le puede ayudar para resolver los ejercicios que se le propongan.
Ley de Dalton:
La ley de Dalton, o ley de las presiones parciales, establece que la presión total de una mezcla de gases es la suma de las presiones que cada gas ejercería si estuviera sólo. Dos sustancias gaseosas A y B, dentro de un volumen V (común):
y 
de acuerdo con Dalton:
: 
Además:
de donde se concluye que: PA = XA PT y PB = XB PT
Las presiones parciales de los gases de una mezcla son iguales a los productos de sus fracciones molares respectivas por la presión total de la mezcla.
Gas real.
Las sustancias reales que cambian fácilmente de fase sólida a líquida y a gaseosa (agua, sustancias refrigerantes, amoníaco), no pueden ser tratadas como gases ideales en general. Sus ecuaciones de estado resultan muy complicadas y sus propiedades termodinámicas son presentadas en forma de tabla.
Para explicar las diferencias en el comportamiento de los gases reales con respecto a los gases ideales, se han dado históricamente diversas aproximaciones. Sólo como aspecto para que puedan ampliar en esto se muestra la ecuación de van der Waals:
La ecuación de van der Waals, fue presentada en 1873 como un perfeccionamiento de la ecuación de gas ideal. La ecuación de estado de van der Waals es:
La constante b es la corrección por el volumen ocupado por las moléculas, y el término a/v2 es una corrección que toma en cuenta las fuerzas de atracción intermolecular. Como podría esperarse en el caso de una ecuación generalizada, las constantes a y b se evalúan a partir del comportamiento general de los gases. Estas constantes están relacionadas con las propiedades críticas del gas. Recordemos que desde el punto de vista de la temperatura, el punto crítico representa la temperatura máxima a la cual un elemento permanece en estado líquido, y la presión crítica, es la presión medida a esta temperatura.
Hay disponible una calculadora para los gases utilizando la ecuación de van del Waals.
Las constantes de los valores de van der Waals se pueden calcular a partir de las constantes críticas de un gas:
Hay otras ecuaciones de estado que se han derivado para los gases reales, pero para nuestros fines, la mostrada resulta suficiente.
Los parámetros reducidos: Son condiciones de temperatura, presión y volumen corregidas o normalizadas, mediante la división entre sus condiciones críticas:
Ley de los estados correspondientes: Un estudio demuestra que si dos o más sustancias cualesquiera tienen la misma presión reducida p, es decir, sus presiones son la misma fracción o múltiplo p de sus presiones críticas respectivas, se encuentran a temperatura reducidas iguales , siendo sus temperaturas las misma, fracción o múltiplo de sus temperaturas críticas respectivas, entonces su volumen reducido será igual. Se dice entonces que las sustancias se encuentran en estados correspondientes.
Factor de compresibilidad
En términos matemáticos se puede indicar que:
En donde k es cierta constante. Esta relación funcional, que se puede aplicar a muchas sustancias pues no dependen de constantes específicas es denominada ecuaciones de estado generalizadas.
El factor de compresibilidad Z es un factor que compensa la falta de idealidad del gas, así que la ley de los gases ideales se convierte en una ecuación de estado generalizada:
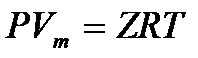
Donde Vm es el volumen molar.
Para un gas ideal la variable Z siempre vale uno, en cambio para un gas real, Z es diferente que uno.
Un gráfico de compresibilidad generalizado representa los valores para los valores reducidos de las condiciones que presente un gas, estos gráficos pueden ser utilizados para determinar el valor de Z, con margen de error, el cual suele ser despreciable. En estos gráficos se presentan con los valores reducidos, la presión reducida en el eje X, el factor de compresibilidad en el eje y los valore reducidos de temperatura y/o volumen en curvas de igual valor. Estos gráficos permiten hacer los cálculos para los gases reales.
Ejemplo: Haciendo uso de las gráficas de factor de compresibilidad que se adjunta, resuelva el siguiente problema.
Cierto gas se encuentra en un recipiente de 10 lits. A 134 atm. Y 20oC. El gas se expande hasta un volumen de 20 lits con una presión final de 50 atm. Determine la temperatura a la se encontrará. Para este gas Pc=33,5 y Tc=195oK
Datos:
T=20oC; Tc=195oK ; P=134 atm; Pc=33,5 atm; V=10 ltd.
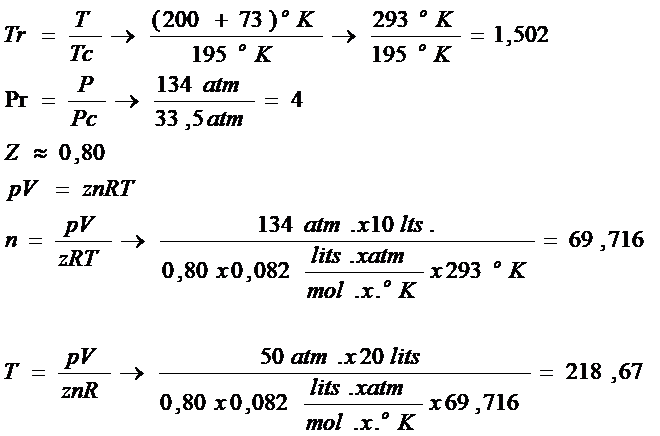
Nota: Algunas ilustraciones han sido tomadas de textos abiertos, propietarios de los derechos de autor de los mismos.
Como los cálculos con el factor de compresibilidad no estan exenos de cierta dificultad, pueden ampliar sobre ello en una página que incluye ejemplos. De la UNAM hay una aplicación para calcular propiedades de los gases reales con distintos comportamientos, que incluye al factor de cmpresibilidad.