Sistemas de coordenadas en el espacio

Coordenadas cartesianas.

Las coordenadas son grupos de números que describen una posición: posición a lo largo de una línea, en una superficie o en el espacio. 

Así en el eje de los números reales, x=4 se indica de la siguiente manera:

Este tipo de sistema de coordenadas lo asociamos con el conjunto de los números reales R. Similarmente, cuando nos propongamos analizar un fenómeno en que se involucran dos variables (que es el caso del plano), denotaremos el conjunto de los valores que pueden tomar ambas, como pertenecientes a subconjuntos de R². Ya en el espacio estableceremos algo similar para R³. No hay que tener mucha imaginación para deducir que se puede hablar de espacios n-dimensionales en que los valores de las variables de una función los asociaremos con subconjuntos de Rⁿ.

Las coordenadas cartesianas o rectangulares son un sistema de coordenadas formado por dos ejes en el plano, tres en el espacio, mutuamente perpendiculares que se cortan en el origen. Recordando un tanto aspectos ya por Ustedes estudiados, en el plano las coordenadas cartesianas x e y se denominan respectivamente abcisa y ordenada. Las ecuaciones de los ejes x e y son respectivamente y=0 y x=0, rectas que se cortan en el origen O cuyas coordenadas son, obviamente, (0,0). Los ejes dividen el espacio en cuatro cuadrantes en los que los signos de las coordenadas alternan de positivo a negativo. Las coordenadas de un punto cualquiera vendrán dadas por las proyecciones del segmento entre el origen y el punto sobre cada uno de los ejes.

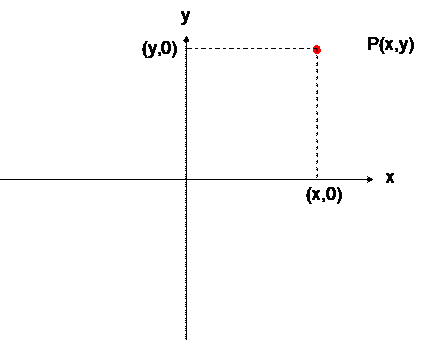
En el plano hay otra forma de expresar la posición de un punto, que son las coordenadas polares. En este sistema se indica la distancia del origen de coordenadas al punto, r, y el ángulo que forma esa recta con el eje x, q. En la siguiente figura se muestra esto y las ecuaciones que nos permiten expresar las ecuaciones en un sistema dado que se conozcan en el otro:

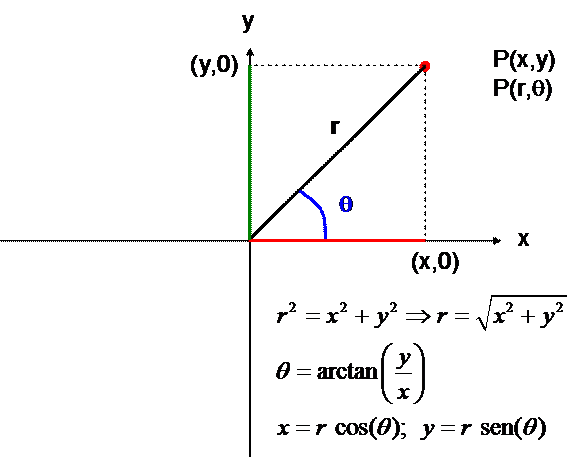
En el espacio 3D, la posición de un punto en coordenadas cartesianas, vendrá dada por un trío ordenado de números que nos indicarán los valores de x, y y z, en ese orden:

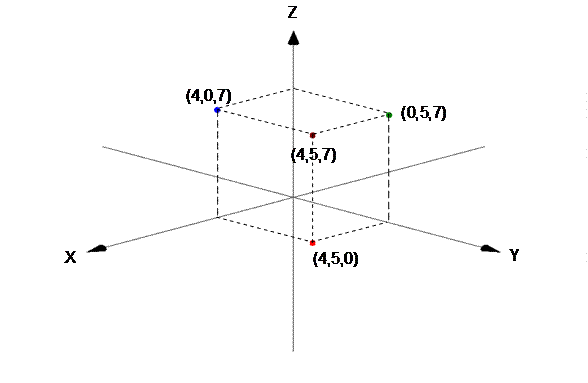
Los planos de referencia XY (z=0) XZ (y=0) e YZ (x=0) dividen el espacio en 8 octantes en los que como en el caso anterior los signos de las componentes cambian de positivo a negativo según sean los valores de las tres coordenadas.

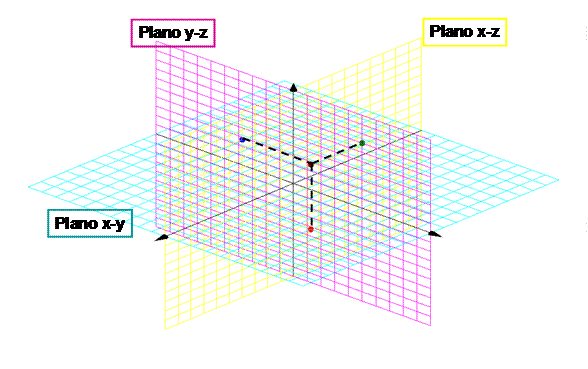
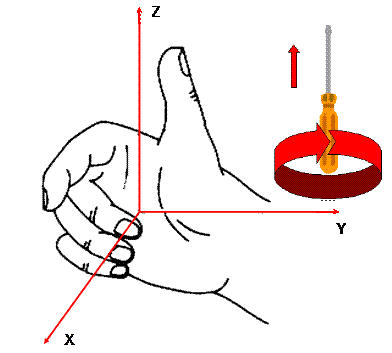
Resulta conveniente señalar que estamos hablando de un sistema de coordenadas al que le es aplicable la regla de la mano derecha, o sea, que z es positivo en la dirección en que avanzaría un tornillo si giramos el mango de un desarmador en el sentido del eje x al eje y:

Muchas de las formulas que Ustedes conocen del espacio  R², tienen su extensión en el espacioR³. Así por ejemplo la distancia entre dos puntos en el plano es:

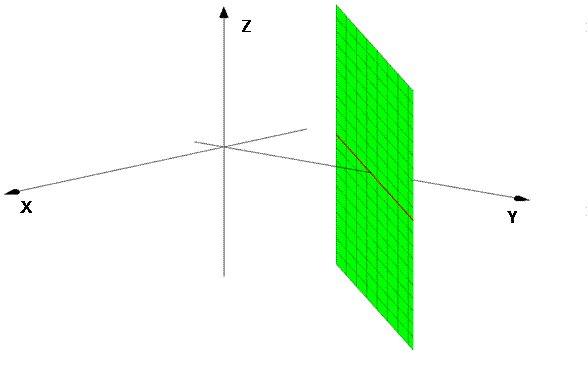
No obstante debemos tener cuidado al extender un concepto del plano al espacio tridimensional. Así por ejemplo la ecuación y = 2x + 5 nos indica en el plano una recta con pendiente 2 e intercepto con el eje y en 5. Sin embargo, si graficamos esta ecuación en 3D, dado que no asignamos ningún valor de z, esta coordenada puede tomar cualquier valor y vamos a tener un plano que contiene a todas las posibles rectas con la proyección y = 2x+5 en el plano (x,y) y todos los posibles valores de z en el intervalo en que consideremos que se encuentren:

Coordenadas cilíndricas y esféricas

Las coordenadas cilíndricas y esféricas constituyen generalizaciones de las coordenadas polares en el espacio tridimensional.

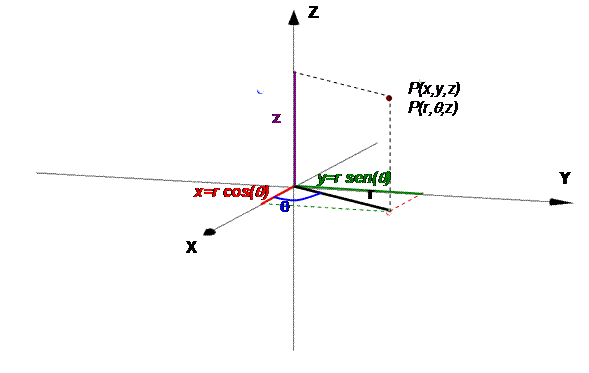
En el sistema de coordenadas cilíndricas un punto  P  del espacio se representa por un trio ordenado  (r, q, z),  tal que:

v     (r, q)  es una representación polar de la proyección de P en el plano XY.

v     z es la distancia de (r, q) a P.

r puede tomar los valores desde 0 a ∞. Los valores de q estarán entre 0 y 2p.

El nombre de coordenadas cilíndricas se origina del hecho de que la gráfica r = c es un cilindro circular recto. Las coordenadas cilíndricas se utilizan con frecuencia en aquellos problemas reales en los que existe un eje de simetría.

En el sistema de coordenadas esféricas un punto P del espacio se representa por un trío ordenado (r, q, f) donde:

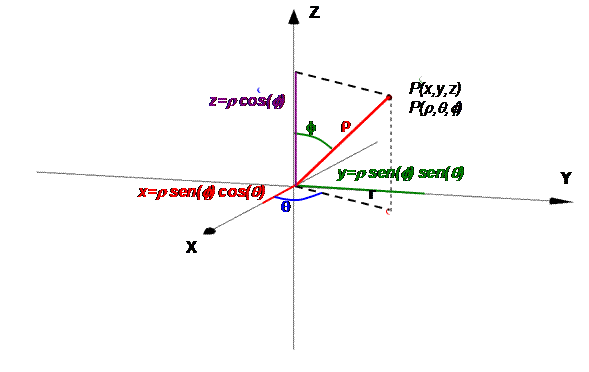
v     r  es la distancia orientada desde O hasta P, (valores de r ³ 0).

v     q  es el mismo ángulo que el usado en coordenadas cilíndricas, (0 £ q < 2 p).

v     f  es el ángulo entre el eje z  y el segmento O- r, (0 £  f  £  p).

Resumiendo:

Coordenadas:      CARTESIANAS           CILÍNDRICAS                         ESFÉRICAS

                                     (x, y, z)                              (r, q, z)                                     (r, q, f)           

         Valores posibles:        (-∞ a ∞)                 0<r<¥,0<q<2p,-∞£z£∞           0<r<¥,0<q<2p,0<f<p

Fórmulas para la transformación de coordenadas

Ejemplos:

Determinar las coordenadas cilíndricas y esféricas del punto (2, -1, -4):

R/ cilíndricas (2.2361, 26.57°,-4); esféricas (4.5826, 26.57°,150.79°):

Determinar las coordenadas cartesianas del punto (5.4, 112°, 3) en coordenadas cilíndricas:

R/ (-2.0, 5.0, 3.0)

Determinar las coordenadas cartesianas del punto (5.7, 22°, 70°) en coordenadas esféricas:

R/ (5.0, 2.0, 2.0)

Para la conversión entre los distintos sistemas de coordenadas pueden utilizar la aplicación correspondiente de Calc 3D, también disponible en línea.

Los diferenciales de volumen: Posteriormente vamos a aplicar, al ver integrales triples, los diferenciales de volumen expresados en coordenadas cilíndricas y esféricas. Al respecto, pueden consultar un material de la Universidad Autónoma del Estado de México que les permitirá ampliar sobre los sistemas de coordenadas y los diferenciales de longitud, área y volumen en los mismos.

En coordenadas cilíndricas el diferencial de volumen es dV = rdrdqdz y en coordenadas esféricas dV = r²senfdqdfdr.

Para el estudio independiente.

Practicar los conceptos con un grupo de ejercicios resueltos de un profesor de Colombia.

Para ver las relaciones entre los distintos sistemas de coordenadas, pueden ver unas páginas interesantes con Geogebra para cilíndricas y para esféricas.

Nota: Los conocimientos de trigonometría son básicos para esta asignatura. El que no recuerde los conceptos de las funciones trigonométricas elementales (seno, coseno, tangente), debe suplir esto con estudio independiente. Les adjunto un material que creo les puede ser útil sobre las funciones trigonométricas básicas. Le sugiero ver una animación sobre esto tomada del Proyecto Descartes.